Combinatorics Decoded-Master Permutations & Combinations
Discover counting principles and combinatorics from Scratch
What you will learn
Fundamental Principal of Counting.
Meaning of Factorial
Arrangement of Objects: Box Method of Arrangement
Arrangement of Objects around a circular Table: Circular Arrangements
Selection of Objects.
Different cases of Permutations such as word formation, Circular Permutations, etc.
Different cases of Combinations such as selection of teams.
Division and Arrangements in Groups
Prime Factorization Theorem and Exponent of Prime p in n!
Some other important results and Many More Problems
Fibonacci Sequence
Golden Ratio
Recurrence Relations and Solving Recursive Relations
Why take this course?
What is Combinatorics?
Combinatorics is a young field of mathematics, starting to be an independent branch only in the 20th century. However, combinatorial methods and problems have been around ever since. Many combinatorial problems look entertaining and one can easily say that roots of combinatorics lie in mathematical creativity and games.
Our lives are full of combinations. Combinatorial mathematics is just the science to deal with combinations of discrete items. As an ancient field, the history of combinatorial mathematics can be traced back over 4000 years to the age of the Great Yu in ancient China. Today, combinatorial mathematics is regarded as the basis of computer science since the algorithms in programming heavily rely on the analysis of discrete elements.
We want to arrange elements in a set into patterns satisfying certain rules. Is this possible? Under which conditions is it possible? What are necessary, what sufficient conditions? How do we find such an arrangement? Enumeration: Assume certain arrangements are possible. How many such arrangements exist? Can we say “there are at least this many”, “at most this many” or “exactly this many”? How do we generate all arrangements efficiently?
This course deals with concepts required for the study of Probability and Statistics. Statistics is a branch of science that is an outgrowth of the Theory of Probability. Permutations and Combinations are used in both Statistics and Probability; and they, in turn, involve operations with factorial notation.
This 50+ lecture course includes video explanations of everything from Permutations and Combinations, and it includes more than 60+ examples (with detailed solutions) to help you test your understanding along the way. Become a Permutations and Combinations Master is organized into 8 sections.
What you’ll learn:
Fundamental Principle of Counting
Factorial
Permutations including Circular Permutations
Combinations
Application to Number Theory
Division into Groups
Arrangements in Groups
Derangements
Multinomial Theorem
Number of Rectangles and Squares
Exponent of Prime p in n!
Important Results to remember
This course is based on a very intuitive book Combinatorics Decoded authored by A. K. Pandey available on the Kindle store and is ideal for students who are interested in mathematics or computer science.
Enroll today and learn the mathematical theory needed to solve real-world problems!
Charts
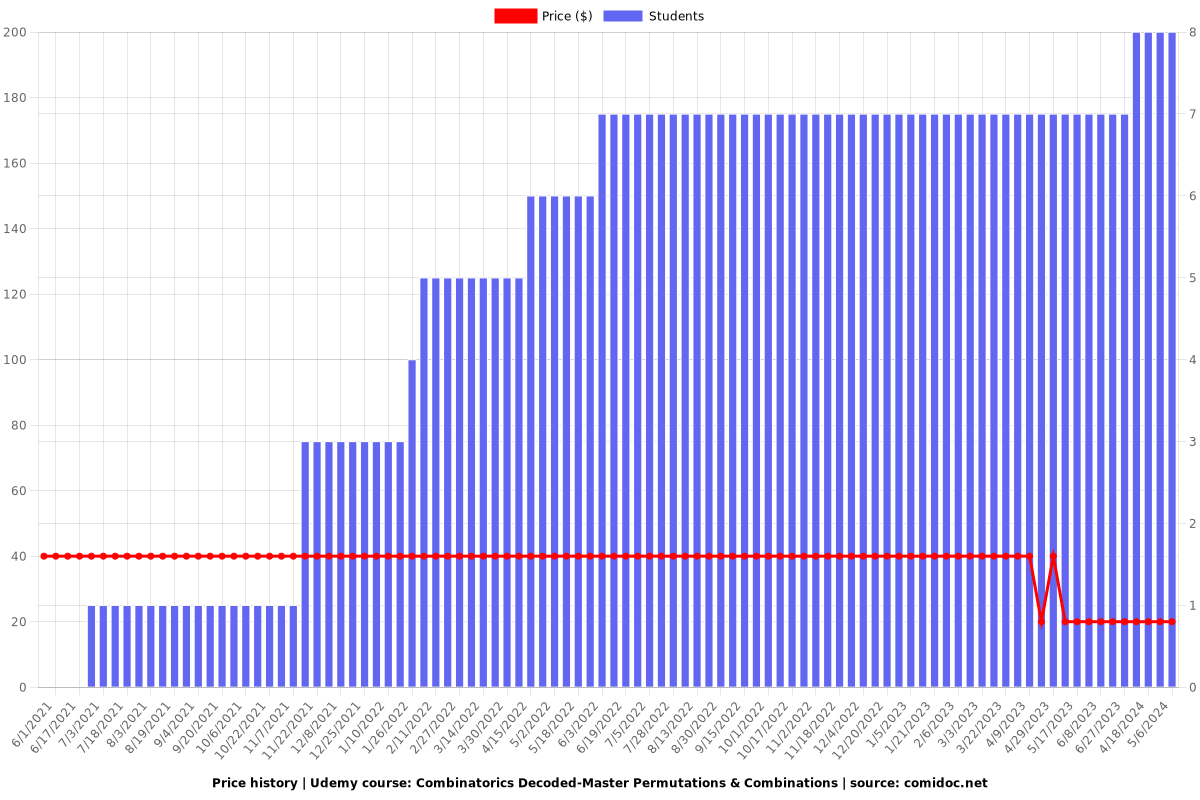
Price
Rating
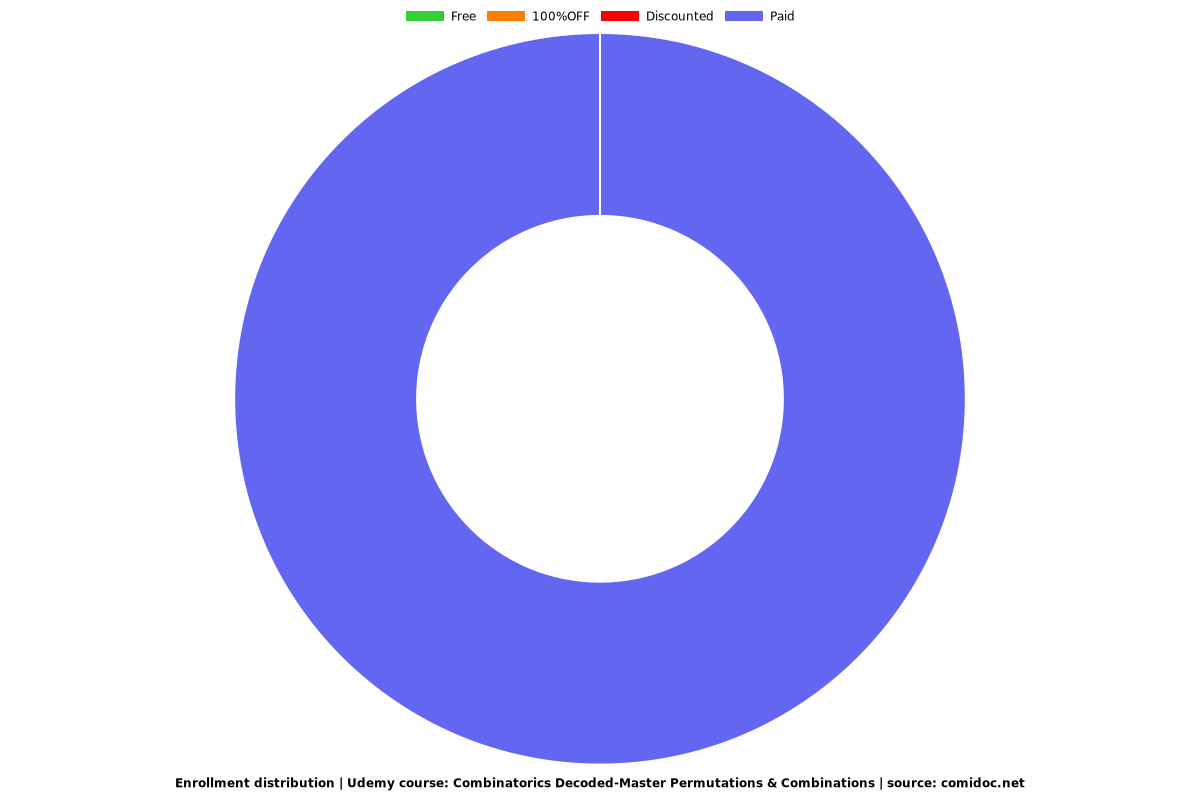
Enrollment distribution